Scalable MinHash Implementation in Python
MinHash algorithm is used to identify near-duplicate documents in a training corpus.
The algorithm is simple:
1 - Partition a document into pieces. For each piece generate H hashes. Choose minimum of the each H hashes across the pieces. Final signature is composed of H hashes.
2 - Compute a signature for all documents in the corpus.
3 - For each document pairs compute a similarity score using Jaccard Similarity based on the signatures.
As part of my training corpus generation studies, I tried to use minhash to de-duplicate documents and I ended up with implementing a scalable min-hash implementation .
Available Implementations
There are numerous options to choose from. I have chosen some of the most approachable e.g. code length and readability.
A Kaggle notebook by Abhishek [1] provides a good starting point. The algorithm being simple but not very scalable. With 32 hashes and 80K documents, tqdm predicted it to run for 15 hours (Will probably ease down but still a lot).
Then I checked Pyminhash by fritshermans [2], but it is not scalable as well. My PC with 32GB of RAM and 32GB VM file, run out of memory with only 80K documents. I tried to modify the code to run on chunks to control memory consumption, but I realized the way the code was implemented did did not allow scaling.
Then I decided to implement my own.
I know there are numerous other options out there that can be tried, but my experiments concluded here, because I like developing algorithms and running complexity studies myself.
Problem Definition
Minhash is a simple algorithm. But it is not very simple to scale up.
3rd step in the algorithm involves pairing each documents which means N^2 time and space complexity (N being number of documents). 3rd step also involves a lot of (N^2) Jaccard similarity computations. It is essential to use an efficient Jaccard similarity computation method.
Efficient Jaccard Similarity Computation
Numpy is great for vectorized calculations. I utilized numpy and left optimization to numpy implementation.
signatures is a numpy array of NxH where N is the number of documents and H is the number of hashes.
For each document signature, take difference between the remaining document signatures in the array. Each zero means a hash match. Count the number of zeros at each row and divide by H to compute the scores.
Note that each step is carried on numpy arrays.
for i in tqdm.tqdm(range(N)):
# broadcast and subtract from the remaining of the matrix
matches = (signatures[i]-signatures[i+1:,:])==0
scores = matches.sum(axis=1) / H
Controlling Memory Consumption
N^2 is an undesirable time and space complexity. While there is no obvious cure to combatting time complexity, there is a way to control memory consumption.
The intuition is that we do not need to store scores for each pairs in the pair cache. We only need scores for the top M pairs. After computing jaccard similarity, we can compare it to minimum jaccard score we have at the time and throw it if it is smaller than the minimum score. If it is larger than the current minimum, we can store it in pair cache and remove the previous minimum from the pair cache. This way we can achieve a pair cache with a maximum size of M.
There are two obvious caveats with this approach and both of them can be mitigated:
- Determining hyperparameter M (pair cache size): It is difficult to determine the hyperparameter M. But we can run the algorithm multiple times with M as large as the system memory allows. After each iteration most similar documents can be removed. Since many documents are removed, the following iteration will be much faster.
When the desired score threshold is found in the pair cache, the procedure can be stopped. Let’s assume 0.6 is the threshold for similarity, the procedure can be stopped when 0.6 is encountered in the pair cache.
- Keeping track of minimums in the pair cache: We need to know current minimum in the pair cache so that we can use to determine whether we should throw a new pair. The naive approach is to sort the pair cache after each insertion. Efficient sorting algorithms can sort a list in
O(mlogm)times. Since the list is sorted beforehand, adding a new element and sorting would haveO(m)time complexity. This is not too bad but there is a better option.
A Perfect Use-case of a Min-Heap
The sorting based approach looks like this. h is a python list that represents the pair cache. Just fill-up the list until it reaches M. Once the list is full, sort the list. Then only add a pair, if its score is larger than the current minimum. If dataset diversity is high, it will not be necessary to add much items at this point.
def add(self, i,j, score):
if self.size < self.limit-1:
self.h.append((score, i,j))
elif self.size == self.limit-1:
self.h.append((score, i,j)) # O(1)
self.h.sort(reverse=True) # O(MlogM)
else:
if self.h[-1][0]<score:
self.h.pop() # O(1)
self.h.append((score, i,j)) # O(1)
self.h.sort(reverse=True) # O(M) (already sorted)
But this solution is not optimal. If M is high and diversity is low, sort will run a lot which will slow down the overall procedure.
At a second glance, we do not need a fully sorted list. We only need to keep track of the current minimum element. This looks like a perfect use case for a min-heap.
This slightly modified version uses the same python list h. List is filled up until the limit. Once the list is full, it is not sorted but heapified meaning it is reorganized to form heap invariant (e.g. parent is smaller than its children).
Here heapify and heappushpop are standard library functions provided by python. While it is easy to implement them, in fact there is no need practical benefit of doing so.
From this point on, if a pair is needed to be stored, it is pushed to the list and minimum item is removed from the heap in a single operation that has a O(LogM) complexity.
This is the best we can hope for and works well in practice.
def add(self, i,j, score):
if self.size < self.limit-1:
self.h.append((score, i,j))
elif self.size == self.limit-1:
self.h.append((score, i,j))
heapify(self.h) # O(N)
else:
if self.h[0][0]<score: # h[0] is the smallest value in the min heap
heappushpop(self.h, (score, i,j)) # O(logN)
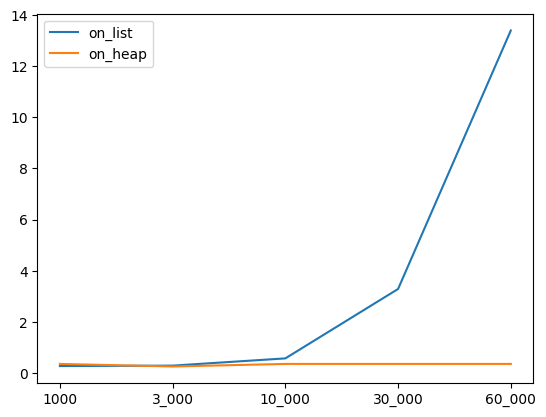
Here is how execution time varies as pair cache size is increased. Heap based approach scales much better, in fact appears to be constant.
Recipe for Duplicate Removal
Assume you know t, threshold value for similarity. Documents with similarity scores larger than t will be removed.
1- Find the right M. Start by using M set to None which means unlimited pair cache, and lower M gradually until your pair cache fits to the memory.
2- Run minhash algorithm with the M hyperparameter.
3- Remove all duplicates documents having a score larger than t.
4- If t is not found in the pair cache, then there might be more duplicate documents in the corpus. Go to step 2.
Details to consider
Total execution time considerations
The pair generation loop iterates over documents and at each iteration calculates scores with the selected document and remaining documents. Since score of doc_a and doc_b is similar to doc_b and doc_a (symmetric property) there is no need to calculate score again for doc_b and doc_a.
For the document 0 there will be N-1 score computations.
For the document 1 there will be N-2 score computations.
. . .
For the document N-2 there will be 1 score computations.
For the document N-1 there will be 0 score computations.
So as the algorithm progresses, each iteration will be faster than the previous iteration. This has no implication on total execution time.
Tqdm is used to visualize the progress. Initial estimation of the tqdm will be much different than the total time actually it will take.
Impact of size of M
If M is None, there will be no bound on the pair cache so there will be no interim sorting (heap operations) operations.
If M is not None, the larger the M, the costlier heap operations will be. Also note that first M items are pushed to the heap without any extra operations.
Very small M may require a second or third iterations of the overall minhash computation procedure.
M is the main hyperparameter to strike a good balance between memory consumption and execution time. I currently do not have the answer to optimal value of M because I haven’t had much chance to play with it.
Results
My very first experiment with applying minhash resulted in an unexpectedly slow performance, taking around 15 hours to process 80K documents with an initial speed of approximately 1.42 iterations per second. I terminated the experiment before it was completed, so I’m unsure what the actual total time would have been.
In contrast, my final optimized implementation finished in just below 1 hour and achieved a significantly faster initial speed of around 12 iterations per second, representing a roughly 10-fold improvement.
Conclusion
The source code can be accessed from my GitHub repository[3].
References
2- Pyminhash