Direct Preference Optimization: Your Language Model is Secretly a Reward Mode
RLHF is used for aligning language models with human preferences. However, RLHF is a complex and often unstable procedure. Proposed algorithm DPO is stable, performant and computationally lightweight. It does not require sampling from the model during fine-tunning or performing significant hyper-parameter tunning. The algorithm tries to solve the RLHF problem with only a simple classification loss which made possible with a new parameterization of the reward model.
Introduction
We may need our language model to recognize common programming mistakes but we do not want it to generate incorrect code. It is important to select desired responses from models wide knowledge base.
RLHF is the most successful class of methods. RLHF involves training multiple LLMs and sampling from the LM policy in the loop of training, incurring significant computational costs.
Proposed method, DPO, does not require explicit reward modelling or reinforcement learning. DPO optimizes the same objective as RLHF (which is reward maximization with KL divergence constraint).
Intiutively, DPO update increases relative log probability of a preferred response to rejected responses. It incorporates a dynamic per-example importance weight to avoid model degeneration.
Preliminaries
Reward Modelling Phase:
Prompt SFT model with prompt x to generate completion y1 and y2. Then humans rank y1 and y2. Preferred response being yw (winning) and dispreferred response being yl (losing).
Preferences are assumed to be generated by a latent model \(r^*(y, x)\) which we do not have access to. Preferences can be modelled using e Bradley-Terry model, according to which human preference distribution p* can be written as:
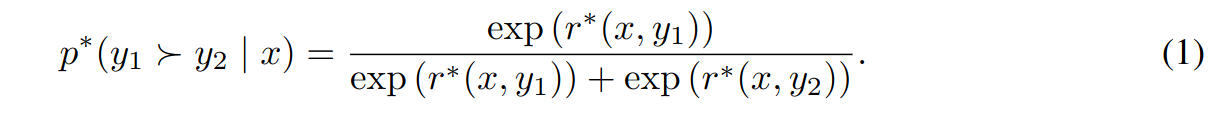
Assuming access to a static dataset D that is sampled from p* it is possible to parameterize a reward model \(r_\phi(x,y)\) and estimate parameters using maximum likelihood. Approching as a binary classification problem, we have negative log-likelihood loss (σ is the logistic function):
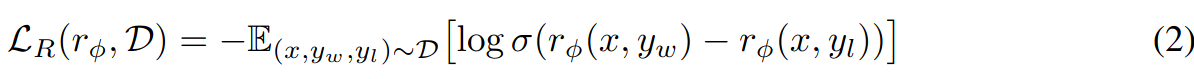
In the context of language models, \(r_\phi(x,y)\) is initiated from SFT model by adding a linear layer on top that produces a single scalar reward value. In order to have less variance on the generated reward, reward is normalized to have an expected value of 0.
RL Fine-tuning Phase
RLHF objective:
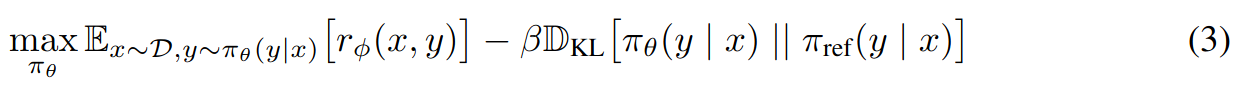
where beta is parameter controlling the deviation from the base reference policy \(\pi_{ref}\), which is the initial SFT model \(\pi^{SFT}\). The constraint (KL divergence constraint) is important to:
- prevent model from deviating too far from the distribution where reward model is accurate.
- maintaining generation diversity
- preventing mode collapse to single high-reward answers.
Due to discrete nature of language generation, this objective is not differentiable and is typically optimized using RL.
Reward function is consructed in the following way and PPO is used to optimize. Note that KL divergence constraint term is expanded as difference of logs.
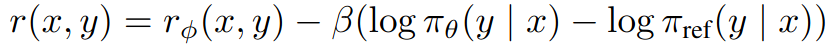
Direct Preference Optimization
In the proposed approach, loss function over reward functions is transformed into loss function over policies. After this modification, it is no longer necessary to model a reward function. Human preferences are still used for optimization. In this approach, the policy network represents both the language model and the reward which is implicit.
Deriving the DPO objective
The optimal solution to the KL-constrained reward maximization objective in Equation 3 takes following form:
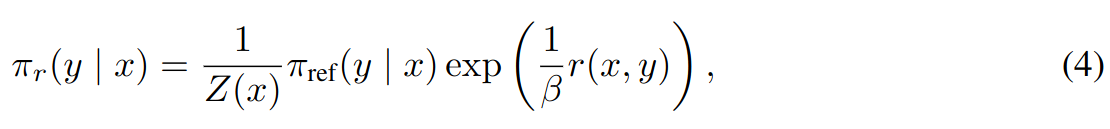
Where Z(X) is the partition function.
In equation 4, take log of both sides and leave reward function alone.
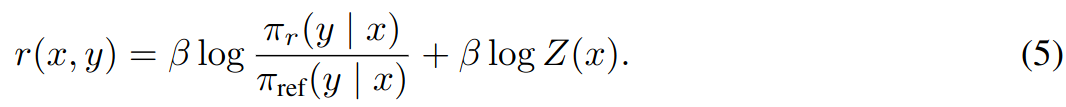
Substituting the reparameterization in equation 5 into the preference model in equation 1, the partition function cancels, and now it is possible to express human preference probability in terms of only the optimal policy \(\pi^*\) and reference policy \(\pi_{ref}\). As a result, the optimal RLHF policy \(\pi^*\) under the Bradley-Terry model satisfies the preference model:
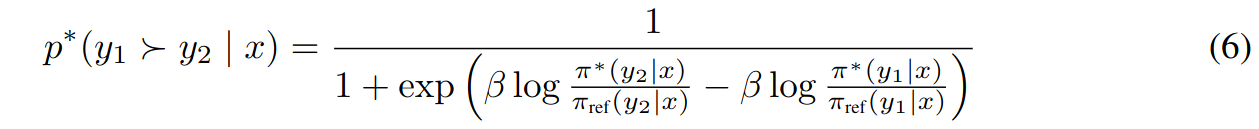
Maximum likelihood objective for a parameterized policy \(\pi_\theta\):
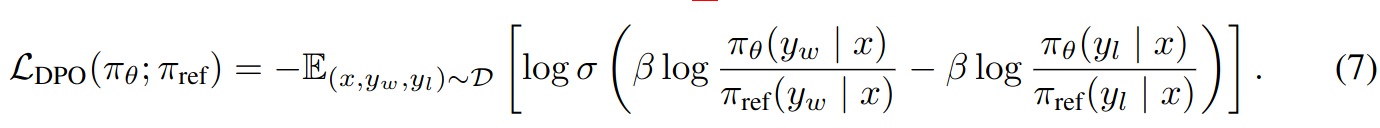
Equation 7 resembles equation 2 where reward based log-likelihood loss is defined.
In equation 7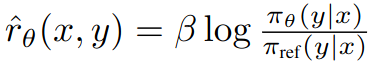 
can be viewed as implicit reward function.
What does the DPO update do?
Gradient of the DPO loss function with respect to parameters θ is:
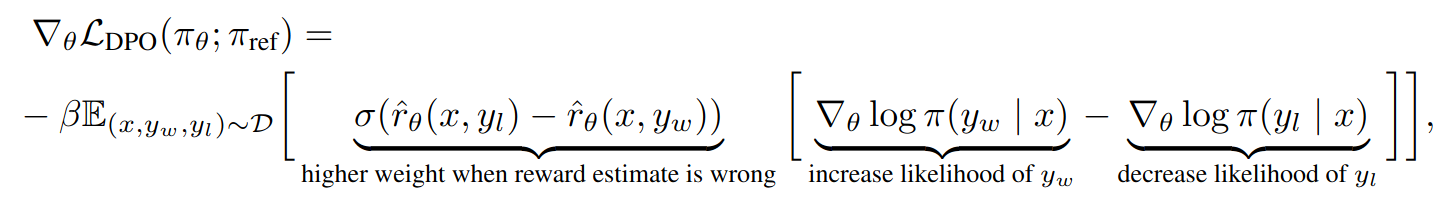
Intiutively, gradient of the loss function increases the likelihood of the preferred completions and decreases the likelihood of dispreferred completions. Importantly, the examples are weighted by how much higher the implicit reward model \(\hat(r)_\theta\) rates the dispreferred completions, scaled by β, i.e, how incorrectly the implicit reward model orders the completions, accounting for the stregth of the KL constraint. Experiments show that this weighting prevents model degeneration.
DPO Outline
General DPO pipeline:
- Sample completions y1, y2 from reference policy (e.g. SFT model), for each prompt x. Label completions with human preferences to construct the offline dataset of preferences, D.
- Optimize the language model \(\pi_\theta\) to minimize DPO loss for the given \(\pi_\ref\) and dataset D and desired β.
In practice, one would like to reuse prference datasets publicly available, instead of creating a new preference dataset. Since preference datasets are sampled using \(\pi^{SFT}\), we initialize \(\pi_{ref} = \pi^{SFT}\) whenever available. However, when \(\pi^{SFT}\) is not available, we initialize \(\pi_{ref}\) by maximizing likelihood of preferred completions (y, yw), that is, \(\pi_{ref} = arg max E_{x, y_w ~ D} [ log \pi (y_w, x) ]\), which is analogous to Supervised Fine-Tuning. This procedure helps mitigate the distribution shift between true reference distribution which is unavailable, and \(\pi_{ref}\) used by DPO.
Experiments
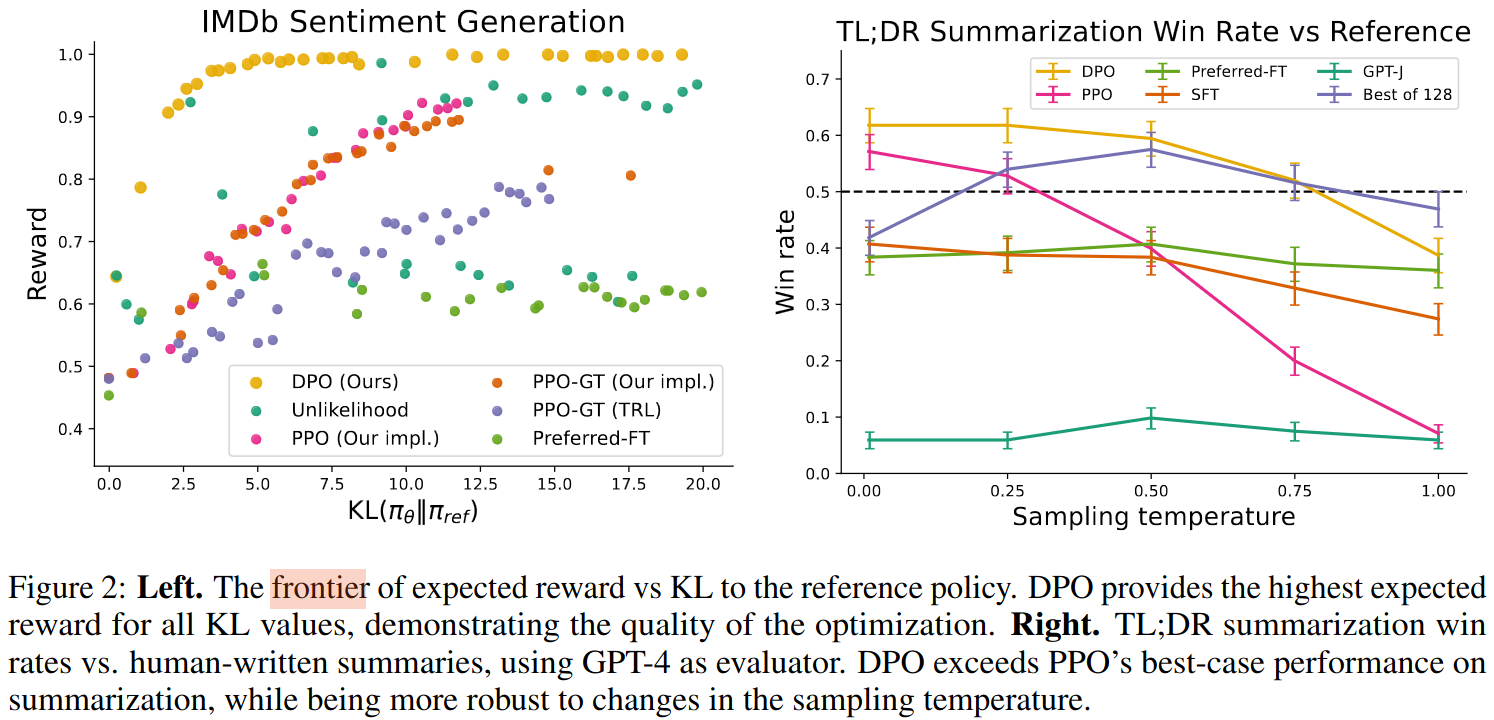
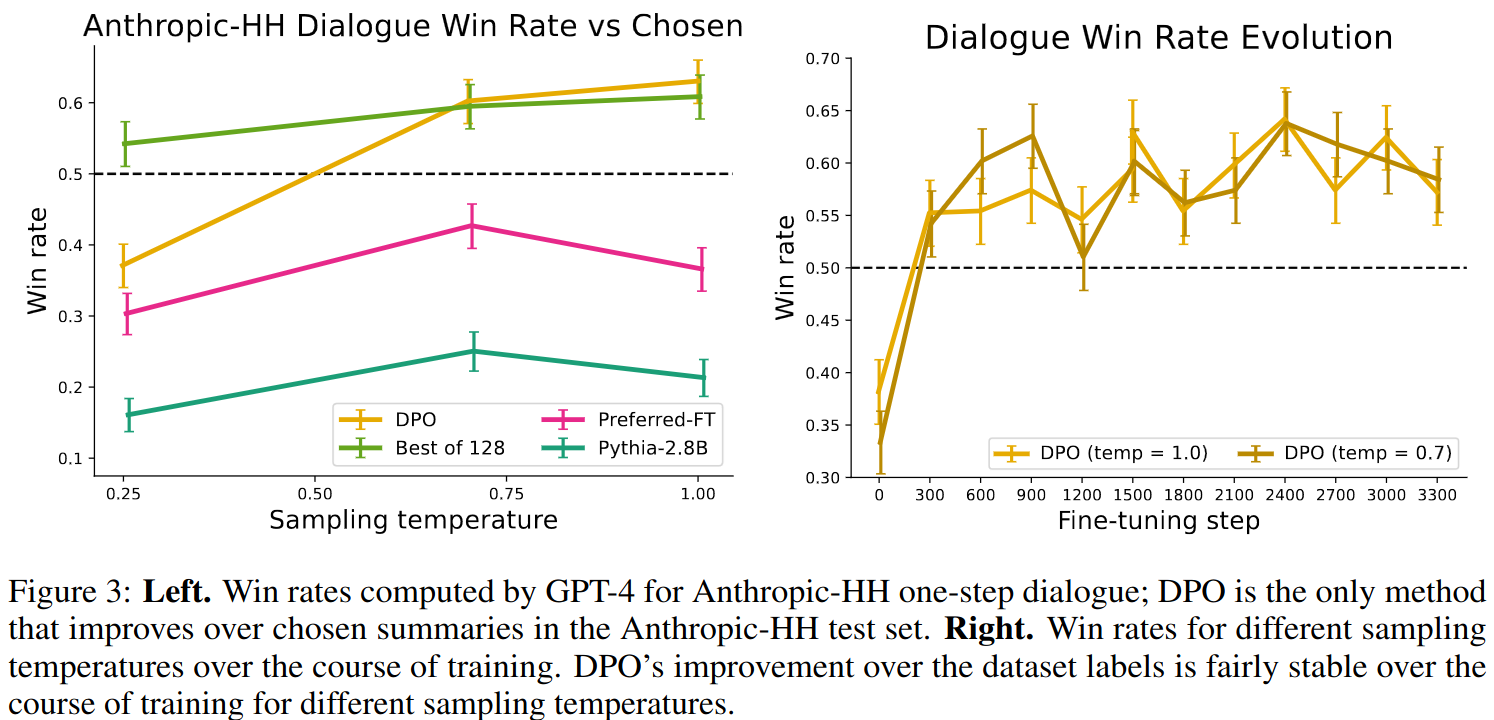
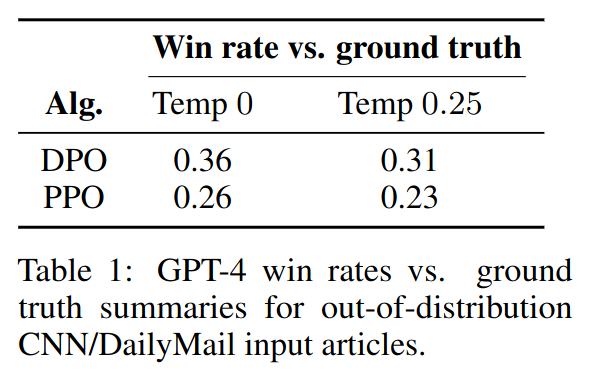
Appendices
DPO Loss Code for PyTorch
import torch.nn.functional as F
def dpo_loss(pi_logps, ref_logps, yw_idxs, yl_idxs, beta):
"""
pi_logps: policy logprobs, shape (B,)
ref_logps: reference model logprobs, shape (B,)
yw_idxs: preferred completion indices in [0, B-1], shape (T,)
yl_idxs: dispreferred completion indices in [0, B-1], shape (T,)
beta: temperature controlling strength of KL penalty
Each pair of (yw_idxs[i], yl_idxs[i]) represents the
indices of a single preference pair.
"""
pi_yw_logps, pi_yl_logps = pi_logps[yw_idxs], pi_logps[yl_idxs]
ref_yw_logps, ref_yl_logps = ref_logps[yw_idxs], ref_logps[yl_idxs]
pi_logratios = pi_yw_logps - pi_yl_logps
ref_logratios = ref_yw_logps - ref_yl_logps
losses = -F.logsigmoid(beta * (pi_logratios - ref_logratios))
rewards = beta * (pi_logps - ref_logps).detach()
return losses, rewards
Hyperparameters
β = 0.1, batch size of 64 and the RMSprop optimizer with a learning rate of 1e-6 by default. Linearly warmup the learning rate from 0 to 1e-6 over 150 steps. For TL;DR summarization, β = 0.5.