Complex Numbers

Standard Form

\(z = x + iy\)

x is real part y is imaginary part

Polar Form

\[cos(\theta) = \frac{x}{r}\] \[sin(\theta) = \frac{y}{r}\]

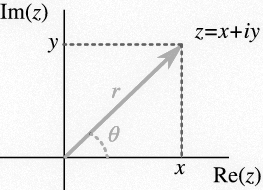
Then:

\[x = r \cdot cos(\theta)\] \[y = r \cdot sin(\theta)\] \[z = x+iy\] \[z = r \cdot cos(\theta) + i \cdot r \cdot sin(\theta)\] \[z = r ( cos(\theta) + i \cdot sin(\theta) )\]

CIS Form

\[z = r \cdot cis(\theta)\]

Exponential Form

\[z = r \cdot e^{i \theta }\]

Euler’s Formula

\[e^{i\theta} = cos( \theta ) + i sin( \theta )\]