Leetcode: Search a 2D Matrix:2

Problem Description

Problem definition is taken from leetcode.

• Search a 2D Matrix 2

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

  Example 1

  

  Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
  Output: true
  

Example 2

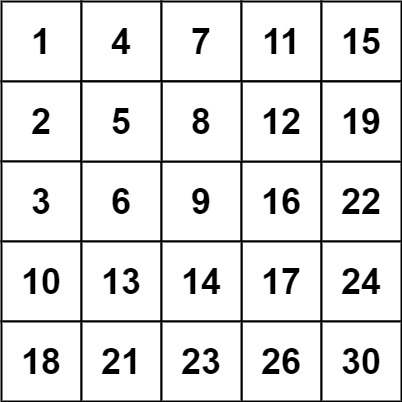
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Solution 1

Start from bottom-left corner. First do binary search in row on the left and then in column on top.

Time complexity is O(max(n,m)*logmn). Space complexity is O(log max(m,n)).

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        return self.search_on_corner(matrix, target)
    
    def search_on_corner(self, matrix, target):
        diagonal_max = min(len(matrix), len(matrix[0]))
        for d in range(max(len(matrix), len(matrix[0]))):
            if d<diagonal_max and matrix[d][d]==target:
                return True
            
            is_found = False
            
            if d<len(matrix):
                is_found = self.bs_row(matrix, d, 0, min(d,len(matrix[0])), target )
            if not is_found and d<len(matrix[0]):
                is_found = self.bs_col(matrix, 0, min(d, len(matrix)), d, target)
            
            if is_found:
                return True
        
        return False
            
    
    def bs_row(self, matrix, i, j0, j1, target):
        
        if j0>=j1: return False
        
        middle = (j0+j1)//2
        
        if matrix[i][middle]==target:
            return True 
        elif matrix[i][middle]>target:
            return self.bs_row(matrix, i, j0, middle, target)
        else: return self.bs_row(matrix, i, middle+1, j1, target) 

        
    def bs_col(self, matrix, i0, i1, j, target):
        
        if i0>=i1: return False
        
        middle = (i0+i1)//2
        
        if matrix[middle][j]==target:
            return True 
        elif matrix[middle][j]>target:
            return self.bs_col(matrix, i0, middle, j, target)
        else: return self.bs_col(matrix, middle+1, i1, j, target) 

Solution 2

This approach considers the matrix is a binary tree whose root node is top-right corner. Left of the tree is smaller and right of the corner is larger. Doing a binary search in the tree will end in the target element.

Time complexity is O(m+n) and space complexity is O(1).

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        row = 0
        col = len(matrix[0])-1
        
        while row<len(matrix) and col>=0:
            if matrix[row][col]==target:
                return True
            elif matrix[row][col]<target:
                row+=1
            else:
                col-=1
        
        return False